I've never seen this topic discussed in collecting forums, or even mentioned online.  This could have made for a nice paper (or eZine article), but I figured it'd make for a good Friday post.  

So, for those not familiar with statistics, a Normal Distribution (Bell Curve) is used to explain many naturally occurring phenomenon.  It is symmetric around the mean. For example, height, intelligence, income, etc. all tend to follow a Bell Curve.  And in collecting, condition is no different. 

This is the standard Bell Curve, as I would relate it to collecting:



Instead of arguing the exact descriptors here, just realize that "average" condition needs to center at the middle of the curve.  In this case I've called it "Very Good".  And each condition description represents an increase of 1 standard deviation from the mean.  In other words, Good and Near Mint represent a +/- 1 standard deviation from the mean (Very Good).  Acceptable to Mint would be +/- 2 standard deviations from the mean, and Poor to Gem Mint is +/- 3 Std Devs.

Now there is a lot of research out there on Bell Curve statistics, but the following is a great link if you'd like to educate yourself:

https://www.mathsisfun.com/data/s...

This is an important picture from that link:



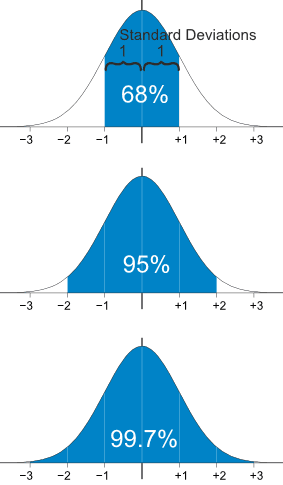
Translating this into our collectibles, you'd expect about 68% of video games to be within Good to Near Mint, 95% between Acceptable and Mint, and 99.7% between Poor and Gem Mint.  And you'd have outliers in the 0.3% leftover, perhaps cash fresh gem mint sealed games or cut rental boxes with sundamage.  

So far, I've just related the bell curve to our hobby, nothing new here.  Now for the next step. Why are Mint games so damn expensive compared to Poor?  Well, it is easy enough to explain with a bit of math.

Let's call the price of a Poor game to be the "Cost of Ownership".  If you can get a poor conditioned, label damaged Little Samson cart for $400, then it costs at least $400 to own a Little Samson cart (that is legit, of course).  For example purposes, let's say price increases by $100 at each condition step... so $500 for Acceptable, $600 Good, $700 VG up to $1000 for Gem Mint (as a cart).  

Now this picture becomes important:



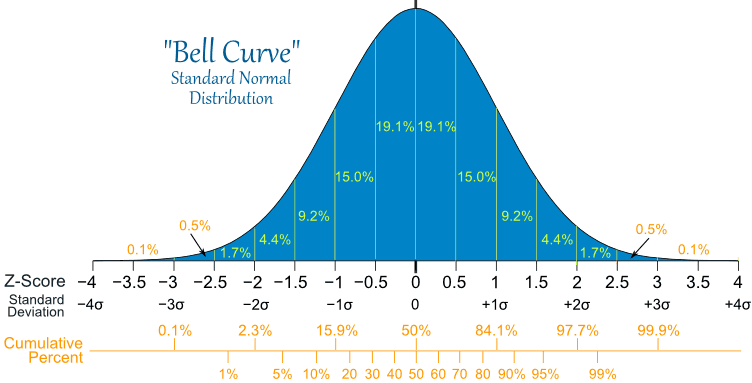
Let's start at -3 Standard Deviations, i.e. "Poor".  We’ll count the bucket around -3, from -2.5 to -3.5.  This produces a value of 0.6% (0.5%+0.1%), meaning 0.6% of collectors willing to pay the cost of ownership for the worst conditioned item.  Now there'd be a lot of guys who would pick up a Poor conditioned item on the cheap (to sell / trade / use as placeholder), but very few would pay the going market rate for it.

Now at the Acceptable level, we count the bucket from -1.5 (4.4%) to -2.5 (1.7%).  Thus 6.1% of collectors would buy an Acceptable game at the Acceptable price.  Repeat the same process and you get 24.2% in Good range, 38.3% in Very Good, 24.2% in Near Mint, 6.1% in Mint and 0.6% in Gem Mint.  Once again, basically mimicking the Bell Curve.

However, what about people who would buy an Acceptable condition game at a Poor price, i.e. the cost of ownership?  All of the Poor collectors would buy it (better condition at same price) and the Acceptable guys would as well (better price at same condition).  Note that the inverse is not true though, as no one would pay the Acceptable price for a poor conditioned item.

So in reality, we’d have the 0.6% of Poor collectors + 6.1% of Acceptable collectors = 6.7% of collectors in the market for an Acceptable condition item at the Poor price.  Of course resellers would have interest as well, but let’s ignore that argument for now.   

And this behavior would repeat up the chart.  Everyone would pay the Poor price for a Gem Mint condition. 
Without using too much math, our previous charts of the Bell Curve are actually the probably density function (pdf) of the Normal Distribution. The behavior we are now describing is the cumulative distribution function (cdf) of the Normal Distribution.  The same data, just this one is presented cumulatively. 



Note the extremely high demand at the best conditioned items, when price is just at the cost of ownership level.  What does this mean?

There are very few collectors at both ends of the spectrum, but for different reasons.  There are few poor collectors because most collectors naturally care about condition.  People may want better condition, but realize they’ll have to pay more for it.  On the Gem Mint side, there are few collectors simply because many people are priced out.  People will accept a lower condition to save themselves some money. 

So this has an important impact on pricing.  If a Poor item gets cheaper, it still does not meet the Acceptable collector’s condition requirements. So they’ll probably drag their feet on the purchase, letting it depreciate some more.  At some point, if the price gets too cheap, then they may eventually buy it as a placeholder and look to upgrade down the road.  But there is no limit on how far that price can fall.

As for the Gem Mint item, let’s say it begins to depreciate.  It will meet the condition requirement for every single collector in the market, so there is natural demand… just many cannot afford it. It has a definite floor at the Mint level of pricing, because the Mint collectors would buy Gem Mint at a Mint price.  It also has one huge factor that a Poor item does not have… upgrade appeal.  When Gem Mint appears, any current owners at lower condition levels may want to purchase the upgrade and sell off their old copy. 

One last point.  You must remember that any collectible hobby can be hot (seller’s market) or cold (buyer’s market) at any given time.  Prices have been up in this hobby for a while, but prices can also fall.   

In terms of our Bell Curve, the items in the middle of the curve will typically follow the overall trend of the hobby.  If it is hot they will appreciate, if it is cold they may stagnate or fall.

Items at the top end of the curve (Gem Mint) may have a chance to at least remain flat, or even appreciate, in a down trending hobby.  Simply because the demand for them is far greater than anything else in the hobby.  The condition appeals to everyone, just not the price of the item.  So thus if the price begins to fall even slightly, someone may consider that a buying opportunity.

And last, you have the items at the bottom of the curve.  They typically only appeal to new collectors who have to have the item, but cannot find a better one (because it is rare), or cannot afford a better one (because it is expensive). And when a hobby does go through a downtrend, this typically coincides with a lack of new demand.  These become the items that stagnate or decrease in price without any bottom in sight.  Although, on a positive note, speculative resellers do actually create a floor here (typically 50% of value).  They are willing to take the gamble and hope that the hobby enters back into an uptrend at some point.

If you made it this far, thanks for reading!  Would love to hear any feedback or comments.  I tried to keep the math simple, but there’s a lot more concepts from calculus and probability / statistics that would apply here.

Yayyyy! Science!

Edit: Solid article. I have very little statistics backround (only what I've needed to pick up on the fly for my research) and I found this pretty easy to read. I've never thought of condition in this respect. I think it makes a good amount of sense. Interesting read. Thanks for posting it!

An interesting read filled with fun pictures. It would get interesting when you throw in personal perception of what 'mint' vs 'gem mint'.

And presumably the multiplier that is applied between each 'level' determined by the individual item and the respective historical costs. I wonder how strong of a coorelation accross platforms (handheld vs console), system (NES vs SNES, etc), etc.

The horror of stats 2507 mixed with my joy of collecting. Jone you truely are an evil mastermind, very good read and very informative! <3

Neat write-up, but don't we have considerable evidence that for boxes, at least, "adequate" is probably the actual average quality, and that the condition of boxes, as they exist today, don't seem to follow a normal distribution?

I would think with any collectible this far after the original production life the curve is going to be biased toward poor/adequate if you're looking at the total population of what is available.




I otherwise agree with your assessment regarding the genuine rarity of the best items and the natural floor relative to other condition classes.

I was under the impression there would be no math on this site.

Good read Jone! While I agree with the assumptions you make using the curves, there isn't any data backing up your claims beyond the assumptions (unless I missed it). Even if you did a modest sample size of a couple common games, you'd start to paint a more accurate account of the collectable market. BUT I will say, that what you have assumed is Gem Mint being outliers although I think you're selling them short to how far out they actually are. Maybe I'm bias BC I really like data so I just wana see more of it

On another not, I love when people say math and its arithmetic. Little things like that make me smile.

A really awesome and insightful post, Jone. I'd love to see this exact principle applied to the whole spectrum of games and not just CIB. Like, I think that the condition of carts matters less to people and the price will fall if the price falls on the whole. But I wonder at what point in the CIB scale would people just rather own a mint cart? I'd guess probably somewhere in the acceptable range.

GOOD GOD MAN, USE NSFW TAGS ON THIS SHIT! WHY DO YOU EVEN HAVE PICS OF SMURF DICKS?!

Talk about a deviation... sicko!

Jokes aside, I learned about bell curves from playing D&D.  So many people claiming to get legit 18s so often, but you never hear about people getting 3s, and they just don't get how common 10-11s would be for stats.
Heck, most people think the average for a six sided dice roll is 3, not 3.5 

I've always struggled with math. You made it easy and understandable. Consider being a math instructor? lol

Probably because they're thinking of the number space between 0 and 6 without considering that the six sided dice goes from 1 - 6.


In terms of stats, I'm guessing it comes down to a version of what everybody does in Wizardry or the TSR AD&D games... that is you re-roll until you get a highly improbable set of awesome stats.

http://www.d20source.com/post/791...
Also, don't know how accurate this is, but "roll 4 and drop the lowest" is going to inherently mean that "3's" are rare compared to the possibility of getting "18's".

A "natural" 18 only needs three 6's out of 4 dice.
A "natural" 3 requires FOUR 1's on the same roll

LOL @ smurf dick.

That was a good read.  I'm not sure if the bell curve is an accurate representation of the value of the pool of games out there, but even if it's not, I agree with your reasoning of why gem mint games retain their value.  IMO, it all comes down to what you said here:

As for the Gem Mint item, let’s say it begins to depreciate. It will meet the condition requirement for every single collector in the market, so there is natural demand… just many cannot afford it. 

Ozzy - D&D definitely helps ingraine statistics into a person.  Everyone knows that the chances of rolling a 3 on a D6 are 1/6, but I'm amazed how many people think that you have a 2/6 chance at rolling a 3 if you get 2 rolls.

I like what your throwing down, though I don't think it works as well with your Samson cart only example as it would for say the box. I don't think the demand for upgrades increases as much for mint cart only, vs mint CIB.

In the manuals, they list diffrent ways you can roll your stats.  By natural, I mean, you roll three 6 sided die, and that's your score, move on to the next.  Wanted to be a fighter but rolled a 7 on strength?  Too bad, you're now a cleric with 12 wisdom.  I've had many people tell me over the years (Mostly in the 90s) that they had 18s doing it this way, normally the story is "Had some amazing rolls, two 18s and a 16" or something like that.

I've never had anyone tell me "Yea we were making chars using the default old school method, and I had a 3 in INT, and 6-8s in everything else.  I couldn't even pick a class."

2nd edition AD&D put this "roll as you go" as method #1, but didn't push it as the go-to way like older editions seemed to.  Then 3rd edition this way kind of went out the window, along with the whole "Don't run a Monty Hall game" way of thinking.
 

I've only ever done one 2nd ed. campaign on pencil and paper, versus the time spent on the TSR games (and those, like Wizardry, you just throw away bad characters until you actually roll something stupendous), so I didn't recall how restrictive the rolling process was versus what sounds like the modern method in that link I found.

Still, I'd expect that they had a friendly DM that just let them reroll a shitty character, or make a few rolls until they got something they liked. (so a lite version of spamming Wizardry characters)

Making somebody play a character where they rolled 3 STR and mediocre everything else is just going to set a bad tone for the whole game, anyway, I'd think, so why start off on such a bad note?
 

this is right in the center of the bell curve entitled "massive amount of time wasted by arch/jone arguing about a pointless topic until they argue about arguing." hey, guys, score that as a natural 20: critical hit.

Awesome post Jone. I love it when people use stats in collecting

Its been on my to-do list for awhile, but has anyone ever taken VGA population reports and used them to come up with the basic distribution of their grades? They obviously tend to get the better conditioned games than are out in the world, but even just using the games that are VGA graded should produce a similar curve among that sample. It would be interesting to see how the mean grades differ between the different systems as well as how the variance changes between them (I would hypothesize that the mean grade would increase and variance would decrease as you move towards the newer generations, but also that there would be a noticeable jump in grades from cardboard boxes to jewel cases and from jewel cases to dvd cases.).

If Joseph Leo where still around, he would surely bust a nut reading your topic.

Not enough talk about precious metals.

 

Or Mandolins

This is why I said "instead of arguing the exact descriptors"....

My "Very Good" is similar to a collector's Very Good as with PSA.  Very Good on PSA is really a 3/10, which I think is a bit too harsh.  

http://www.psacard.com/Services/P...

If you don't like Poor / Acceptable / Good / Very Good / Near Mint / Mint / Gem Mint, then maybe you'd prefer Poor / Acceptable / Fair / Good / Very Good / Excellent / Mint.  

The adjectives themselves do not matter, it just matters that you have 7 names for the mean and standard deviation levels.  Newer stuff like Amiibos would have the center of their bell curve around the Excellent level, while older stuff definitely has a bell curve centered around Average / Good / Very Good, whatever you want to call it.

Well this is just a theory, someone else would have to provide the burden of proof to argue against it.  I'm not saying every exact game (like NWC) or every exact medium (cart vs. CIB vs. Sealed) follows this trend exactly, but this is a good theory regarding the value of collectibles as a whole.

 

Isn't the burden of proof on the person making the claim in the first place?

 

José Pheleo, what a thread!

Did anyone notice JosephLeo pop back the other day to make one of the Iwata threads?

Jone, thanks for posting. I love me some math stuffs.